Ember Coffee Mug Virtual Teardown

Virtual Teardown
When I saw the original advertisement for the Ember coffee mug, I was drawn to it like a Seattleite to a Starbucks. I knew that I had to get one and would then inevitably spend my weekend trying to figure out precisely how it works.
The Ember travel mug is a $149.95 tech version of the venerable hot beverage mug. It has a simple value proposition: with an Ember mug, you can consume your beverage precisely at your personally-selected perfect temperature. Unlike traditional mugs, where the beverage is too hot at the beginning and too cold at the end, an Ember mug gives you the ideal temperature for the entire drinking experience. If you're spending $3.50 a day for such beverages, that's over $1,000 a year. What is $150 for a device that will make each consumption experience perfect?
At $150, though, a real-life teardown would be too spendy for my taste. My alternative was to perform a virtual teardown by making measurements on the mug, speculating how it works, modeling it with PartQuest Explore, and adjusting model configuration and parameters until the simulations and real-life measurements matched. Below is what I discovered.
Ember - Heating and Cooling
An Elegant Design
I was intrigued by the claim that the Ember mug could keep my coffee at the PERFECT drinking temperature. This is trickier than it sounds, since it means that the control system built into the mug would need to both heat and cool the liquid. Most beverage mugs are optimized to simply maintain the existing temperature, typically by thermally insulating the liquid from the outside world. But that means the liquid will start out too hot and then gradually cool, only passing through the ideal temperature briefly.
The Ember mug tackles this problem by providing a mechanism for both heating and cooling. The heating mechanism is a straightforward electro-thermal heating element. But the cooling mechanism is, well, much cooler! The mug uses a patented approach, encasing the mug with a phase change material (PCM). Thermodynamically, the beverage is cooled by transferring energy from the hot liquid to the PCM by progressively melting the PCM (changing its phase from solid to liquid, with the resulting transfer of the heat of fusion from the coffee to the PCM).
Figure 1 shows the major components of the mug, including the phase change material. The overall system is beautifully executed, with an elegant user experience and phone app that is connected via Bluetooth.

Figure 1. Ember Travel Mug Cutaway
The Thermodynamics of Phase Change Materials
Picture the PCM as a jacket of paraffin that quickly starts melting when a hot liquid is introduced into the mug, transferring energy during the phase change (melting). When any solid material is heated, its temperature increases until it reaches the material's unique melting point. Then, even as additional heat is transferred to the material, its temperature remains constant, at the melting point, until all of the solid has become a liquid. For a coffee mug, this means that the hot coffee that is poured into the mug will almost immediately melt the PCM and the coffee will drop in temperature to the melting point of the PCM. Additional heat can then be added to the coffee by the mug's electro-thermal heating system, thereby raising and maintaining the temperature of the coffee (and the liquid PCM) at the desired temperature.
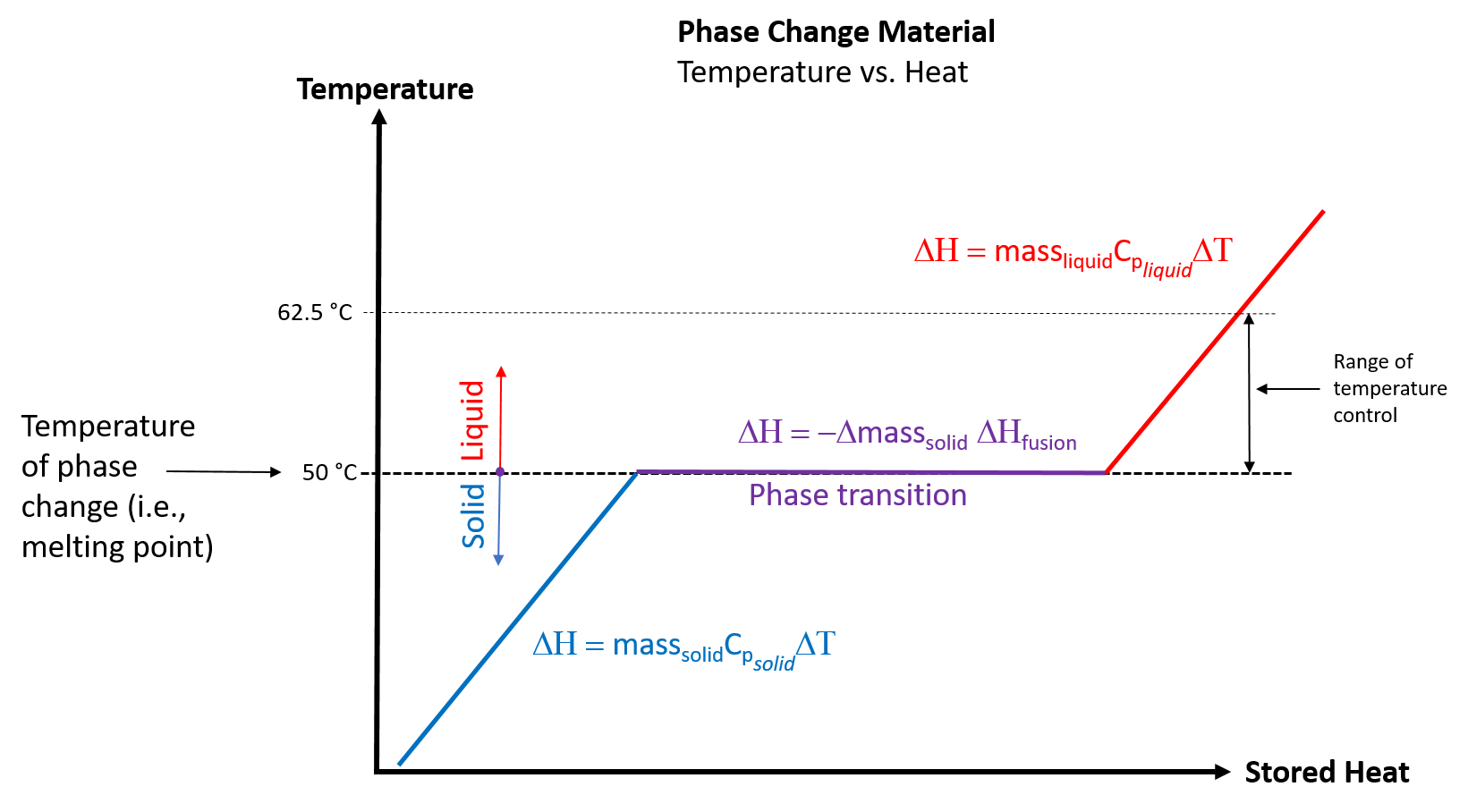
Figure 2. Temperature versus Stored Heat for a Phase Change Material
PartQuest Explore Model as a Virtual Teardown
The PartQuest Explore schematic, below, is a virtual teardown of the mug via a set of PartQuest Explore models. Let me emphasize that this is entirely my conjecture about how the mug's components are functionally related—I don't have any inside information from the people at Ember. The resulting model agrees well with my measured data, so it's possible that I guessed correctly, but it's also possible that other combinations of the configuration and parameters would produce the correct results.
Figure 3. PartQuest Explore Ember Mug System Model (drag probes to see different waveforms)
This model in Figure 3 simulates the process of filling the mug with a hot liquid and maintaining it at the setpoint until the battery is depleted. One of my original reasons for modeling the mug was so I could estimate the impact on battery life of increasing the maximum allowable temperature setpoint (currently 62.5C / 145F). I determined that the maximum could be easily be increased by a few degrees with an acceptable decrease in battery life.
This circuit model includes modeling the PCM. From the measurements used to characterize the actual device (see Figure 4), it appears that the PCM contains multiple melting-point materials: thus two materials were included in the model, at melting points of 47C and 52C. The thermal mass of the liquid is modeled by the block in the diagram with a coffee-cup symbol. The feedback control is simple proportional gain. Since the wall charger output voltage is approximately 20 V and should be slightly higher than the battery pack, it is assumed that the battery pack has 5 Li-ion cells in series for a total battery voltage of ~17 V. The battery cell capacity was estimated, from measurements on the real-life temperature profile over time, at 130 milliamp-hour capacity for each cell, giving a total of 650 milliamp-hours capacity.
The VHDL-AMS language and the PartQuest Explore simulator support the concept of modeling physical systems, including the concept of conservation of energy. This is accomplished via a physical natures language construct: electrical and thermal natures are just two of the many supported natures. The red wires in Figure 3 are for thermal nature modeling, with temperature as the across variable and heat flow as the conserved through variable. Black wires are for electrical nature modeling, with voltage as the across variable and current as the conserved through variable. The green wires are directional control signals (modeling the control system variables). In the real mug, the green signals and their associated blocks are implemented as software and I/O for the mug's microcontroller.
The block labeled “Temp” models the temperature sensor, feeding back the temperature to the proportional controller. The block on the far left is the setpoint, with a step-input from ambient to the desired beverage temperature.
Model Characterization
The purpose of the circuit model in Figure 4 is to calibrate the individual modeling elements that compose the larger circuit, including the thermal impedance of the mug insulation and the phase change materials (PCM) that are used in the Ember mug.
Figure 4. PartQuest Explore Ember Mug Measured Data and Characterization Model (drag probes to see different waveforms)
The following experiments represented by this circuit model were passive - the Ember mug was powered off during all of these measurements so that the intrinsic characteristics of the materials could be observed and characterized.
The temperature represented by the node ember_temp_exper is experimental data collected from an actual Ember mug. For this experiment, 350 ml of water at 81.9C was added to the mug and its temperature was measured over several hours. This data was entered into a PartQuest Explore piece-wise-linear source model so that it could easily be compared to simulations.
The temperature represented by the node insulated_temp_exper is experimental data collected from an ordinary insulated mug of approximately the same size: 400 ml of water at 81.9C was added to this mug and its temperature was measured over several hours. The data was also entered into a source model for easy comparison.
The difference between these two temperatures, ember_temp_exper and insulated_temp_exper, roughly shows the effect of the PCM used in the Ember mug. Even though the water temperature was the same in both at the start (81.9C), the energy required to melt the PCM causes the Ember mug temperature to drop much more quickly than the ordinary insulated mug (the first data point was already down to 77.2C). As the water in each cools, however, the energy from the PCM in the Ember mug is recovered as the temperature drops below the PCM melting point and the heat-of-fusion energy is returned to the liquid. This causes the water temperature in the Ember mug to drop more slowly than the ordinary insulated mug. Note that the difference in temperature narrows between these two after 5,000 seconds (83 minutes).
The thermal network shown in the lower part of the circuit diagram in Figure 4 models the thermal characteristics of the Ember mug. This includes the thermal mass of the water, with its heat capacity (Cp), the two PCM blocks, the thermal impedances, and the ambient temperature reference. The thermal capacitor is used only to establish the initial conditions of the simulation, but it could also be used to model the thermal capacitance of the mug body.
Two instances of the PCM model (see the symbols with a miniature phase change diagram) are used in each of the circuit diagrams. since the experimental data appears to show two distinct inflection points in the temperature decay. This indicates that there are two separate PCM materials with slightly different melting points. This may be by design or it may simply be manufacturing variation.
Conclusion
The virtual teardown was a success! The PartQuest Explore model nicely matched the measured performance of the Ember mug. The phase change material, which is the most novel feature of the mug, was successfully modeled using the IEEE standard VHDL-AMS language. And I saved $150 by avoiding a real-life teardown.
I also verified that the engineers at Ember could increase the maximum temperature setpoint above 62.5C without a significant decrease in battery life. But I suspect that the choice of the maximum temperature setting has more to do with the opinion of an Ember employee regarding the proper temperature at which coffee should be enjoyed.
APPENDIX: Phase Change Material VHDL-AMS Model Code
PartQuest Explore has a large collection of ready-to-use models in a library, so much of the circuit models above could be constructed using off-the-shelf individual models. The library, however, did not include a model for phase change materials. This is an important effect for the Ember mug, however, so I needed to develop a PCM model. The IEEE Standard VHDL-AMS code follows:
------------------------------------------------------------------------------ -- Model Title: Phase Change Material -- Entity Name: Phase_Change_Material -- Author: Darrell Teegarden -- Created: 9/10/2017 1:43 pm -- Last update: ------------------------------------------------------------------------------ -- Description: Phase Change Material -- -- This model represents thermal behavior of a phase change material (PCM), -- where the heat flow through the PCM is related to properties and state of -- the PCM. The model detects the temperature-related phase transitions and -- provides thermodynamic responses that are appropriate to current phase. -- If the material is completely in either the solid or liquid phase, the -- temperature and heat flow are related simply to the heat capacitance of -- the material (Cp). When the material is in the transition between solid -- and liquid, however, the heat flow will be related to the specific -- heat of fusion, for the portion of the mass that is currently transitioning, -- as well as the heat capacity of the portion of the material that are in -- either solid or liquid phases. -- -- During the phase transition, the temperature will not change from the -- melting point of the PCM. -- -- This model can be used in "lumped" thermal networks, -- along with thermal (heat transfer) resistances, heat-flow and -- temperature sources and all electro-thermal elements, to represent -- dynamic thermal systems. -- -- This model can force the initial temperature to the value specified by -- the generic parameter "initial_temperature". It will be enforced by the -- simulator during the "DC" (quiescent_domain) solution, but only if the -- generic parameter "use_initial_temperature" is set to TRUE. -- If "use_initial_temperature" is set to FALSE, the simulator will ignore -- the value of "initial_temperature", and will find the steady-state -- initial temperature based on external thermal circuit constraints. ------------------------------------------------------------------------------ entity Phase_Change_Material is generic (Cp_liquid : real := 4181.3; -- Constant pressure heat capacitance (water = 4181.3) Cp_solid : real := 2050.0; -- Constant pressure heat capacitance (ice = 2050.0) H_Fusion : real := 333.55E3; -- Constant heat capacitance (ice = 333.55K) mass : real := 1.0 ; -- Thermal mass melting_point : real := 0.0; -- Melting temperature of PCM (ice = 0.0) use_initial_temperature : boolean := False; -- Forces delta_temperature = initial_temperature initial_temperature : real := 27.0); -- Initial capacitor temperature port (terminal therm1 : thermal_c); end entity Phase_Change_Material; ------------------------------------------------------------------------------- -- Architecture ------------------------------------------------------------------------------- architecture default of Phase_Change_Material is type phase_state is (solid, phase_transition, liquid); type temperature_state is (T_solid, T_phase_transition, T_liquid); type mass_state is (m_solid, m_phase_transition, m_liquid); quantity delta_temperature across heat_flow_thru through therm1 to thermal_c_ref; quantity heat_flow_fusion : real := 0.0; quantity heat_flow_liquid : real := 0.0; quantity heat_flow_solid : real := 0.0; quantity mass_solid : real := mass; quantity mass_liquid : real := 0.0; signal phase : phase_state := solid; signal t_state : temperature_state := T_solid; signal m_state : mass_state := m_solid; constant epsilon : real := 1.0E-6; begin if domain = quiescent_domain use if use_initial_temperature use -- DC w/initial conditions delta_temperature == initial_temperature; mass_solid == mass; else -- DC w/o initial conditions mass_solid == mass; heat_flow_thru == heat_flow_liquid + heat_flow_solid + heat_flow_fusion; end use; else mass_solid + mass_liquid == mass; -- mass balance heat_flow_thru == heat_flow_liquid + heat_flow_solid + heat_flow_fusion; -- heat balance end use; if phase = phase_transition use delta_temperature'dot == 0.0; heat_flow_fusion == -1.0*H_fusion * mass_solid'dot; heat_flow_liquid == Cp_liquid*mass_liquid*delta_temperature'dot; heat_flow_solid == Cp_solid *mass_solid *delta_temperature'dot; elsif phase = solid use mass_solid == mass; heat_flow_fusion == 0.0; heat_flow_liquid == 0.0; heat_flow_solid == Cp_solid *mass_solid *delta_temperature'dot; else -- phase = liquid mass_liquid == mass; heat_flow_fusion == 0.0; heat_flow_liquid == Cp_liquid*mass_liquid*delta_temperature'dot; heat_flow_solid == 0.0; end use; ---------------------------------------------------------------- -- Process to detect temperature transition at the melting point ---------------------------------------------------------------- Temperature_process: process (delta_temperature'above(melting_point-epsilon), delta_temperature'above(melting_point+epsilon)) is begin if delta_temperature'above(melting_point+epsilon) then t_state <= T_liquid; elsif delta_temperature'above(melting_point-epsilon) then t_state <= T_phase_transition; else t_state <= T_solid; end if; end process; ------------------------------------------------------------------------------------------------- -- Process to detect the transition when phase change is complete, either for freezing or melting ------------------------------------------------------------------------------------------------- Mass_process:process (mass_liquid'above(0.0),mass_liquid'above(mass), mass_solid'above(0.0), mass_solid'above(mass)) is begin if mass_liquid'above(mass) or (not mass_solid'above(0.0)) or (mass_liquid = mass) then m_state <= m_liquid; elsif (not mass_liquid'above(0.0)) or mass_solid'above(mass) or (mass_solid = mass) then m_state <= m_solid; else m_state <= m_phase_transition; end if; end process; ------------------------------------------------------------------------------------- -- Process to manage the phase transition, from solid, to melting/freezing, to liquid ------------------------------------------------------------------------------------- phase_process: process (m_state,t_state) is begin if ( (m_state'event and m_state=m_solid) or (t_state'event and t_state=T_solid) ) then phase <= solid; elsif ( (m_state'event and m_state=m_liquid) or (t_state'event and t_state=T_liquid) ) then phase <= liquid; elsif ( (m_state'event and m_state=m_phase_transition) or (t_state'event and t_state=T_phase_transition) ) then phase <= phase_transition; end if; end process; end architecture default;
Figure 5. Phase Change Model VHDL-AMS Source Code
You can see the source code for any PartQuest Explore model by right-clicking and selecting "View/Copy Model"
- 5131 views
Get the Heat Out! … Electronic-Thermal Design Modeling
We have recently added a number of new electro-thermal models to our Component Library. These models represent devices that are either temperature sensing/control elements, or electronic components that dissipate significant power and may require thermal analysis. These models include:
- Peltier Thermo-Electric Cooler
- Thermistor
- BJT (NPN and PNP)
- MOSFET (N- and P-channel)
- Diode (Rectifier and Zener)
- LED and Incandescent Lamp
- Linear Regulator and OP-AMP
With this new set of models, in addition to our existing passive thermal network elements, our users can more effectively assess the thermal aspects of all their electronic designs, and explore temperature control concepts to mitigate thermal problems.
Modeling Transistor Amplifier Self-Heating using a Thermal Network
The circuit shown above is a very simple transistor amplifier, intended to show the basics of electro-thermal modeling. The "design" includes an 8 Ohm pull-up resistor and an active pull-down NPN BJT. Both of these models are from the “Thermal and Electro-thermal” Category of the Components Library. They both have a thermal port that can connect to an external thermal network, and they output all power dissipated in the device as a thermal heat-flow into that network.
The thermal network includes the heat-sink's heat capacitance (0.1 J/degC) and heat transfer resistance to the ambient (10 degC/Watt). This network configuration represents a system in which the resistor and transistor contribute heat to the same heat-sink, and thermal “cross-talk” or mutual- as well as self-heating is modeled. The transistor's thermal heat-flow path also includes an 8.8 degC/Watt resistance, representing the junction-to-lead thermal resistance published in the device datasheet (see Diodes Inc. FZT869).
From the simulation results it is clear that the heat-sink temperature rises to nearly 120 degC (purple waveform), causing the transistor's junction temperature to approach 150 degC (average, red waveform). This is significantly higher than the value predicted in a companion design example: "Modeling Transistor Amplifier Self-Heating - Hot Part Monitor"). In that system, the two devices are assumed to be thermally isolated, and the steady-state junction temperature < 90 degC.
Electro-thermal Trade-off Analysis for AC-DC Converter with Current Boost Regulator
The second example shows a more practical electronic circuit with electro-thermal aspects modeled. The design is a 5V regulator (non-switching), driven from a 120 Vac/60 Hz input and using a transformer/rectifier circuit to step down to a much lower DC-link voltage. The load current capability is 5A, which is well above the current limit of the linear regular component itself. This is thanks to the load sharing role of the bypass PNP transistor. The design is based on an example application circuit shown in Figure 11 of the On Semiconductor Datasheet MC7800/D, November 2014 - Rev. 27.
All of the power dissipating electronics' models are from the "Thermal and Electro-thermal" Components Library. This includes the rectifier diodes, the linear regulator and the BJT, as well as the current sense resistor and the effective winding resistance of the transformer primary and secondary.
The thermal network includes the heat-sink's heat capacitance (0.1 J/degC) and heat transfer resistance to the ambient (1 degC/Watt), as well as the datasheet published values for the junction-to-lead thermal resistance of each of the active electronic components. An assumed value for the thermal capacitance of the BJT (0.005 J/degC, not provided by the manufacturer) was added for purposes of illustration. Obtaining the actual value would require deeper analysis or measurement of this important component characteristic. However, in this example, both thermal capacitance values were selected solely to give sufficiently fast thermal time constants, so that steady-state operating temperatures could be reached with minimal simulation time.
This design is based on another shared design “AC-DC Power Adapter with Current Boost Regulator”. That design has been modified not only to add the electro-thermal aspects, but it was also adjusted to improve its thermal performance. For example, the DC-link capacitance (c3) was increased from 4700uF to 22000uF, to allow a reduced DC-link operating voltage (i.e. to improve efficiency) while avoiding regulation drop-out at AC zero-crossings under heavy load conditions.
Laser Temperature Regulator System using a Peltier TEC
The third example shows a complete thermal control system in which a Peltier Module, or Thermo-Electric Cooler (TEC), is used to actively transfer heat away from a "laser" or any other electronic device, during fast-changing power dissipation conditions. A thermistor, which has resistance that is highly sensitive to temperature, is used in a Wheatstone bridge configuration. The bridge produces a differential voltage that is amplified by an op-amp circuit. The op-amp output voltage is approximately proportional to temperature over a limited range, and 180 degrees out of phase.
The rest of the control loop is modeled using ideal mathematical control blocks. This abstraction allows the designer to focus on the overall performance of the regulator, and to assess the choice of PID gains during actual transient operation. These gains were selected to ensure stability of the loop using a companion design: Laser Temperature Regulator TDFS. In that design, a TDFS loop-stability analysis is performed at a nominal operating point. But because many of the components in this loop are non-linear in nature (e.g. the TEC, the thermistor/bridge, even the op-amp with rail voltage limiting), it is good practice to simulate performance during large-signal transients, as shown here.
In this case, the drive voltage to the self-heating “laser” (i.e. modeled with the electro-thermal resistor) is step increased to several operating levels (blue waveform), and the temperature of the laser (red waveform) is seen to be held at the regulation set-point of 25 degC, with only momentary disturbances during the power level transitions.
- 96 views

